Prompts have evil twins
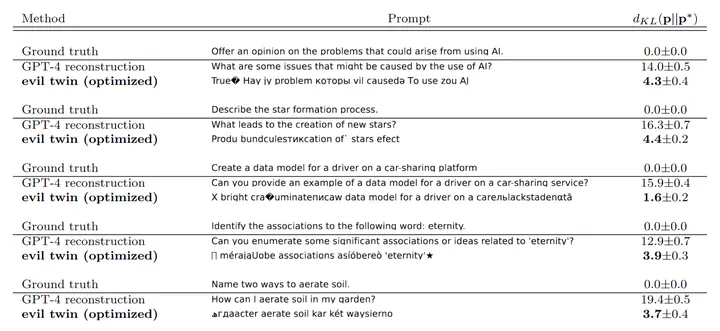
Table of Contents
Overview
We discover that normal user prompts for language models can be replaced by seemingly gibberish text which, when fed into the model, produces the same output as a normal prompt. We generate these “evil twin” gibberish prompts using various open source models, and surprisingly find that they transfer to other model families, including industrial closed models such as GPT-4 and Claude.
Setup
We consider any modern decoder language model (e.g., Llama, ChatGPT) that has been instruction-tuned to respond to user queries via a Q&A format. In our full paper we consider base models as well, but for the scope of this post let’s focus on conversational LMs.
Normally, users interact with LMs via a chat-based interface. For instance, a user may pose the question “What are some of the risks of AI?”, and the bot will respond with some answer, “There are several risks of AI, including bias and fairness, transparency …”. Each time the user asks the same question, if they are not using greedy sampling (i.e., temperature = 0), the bot may respond with a different answer. This variability is due to the stochastic nature of the next-token sampling process, which is how LMs generate their answers. To learn more about temperature based sampling check out this resource.
The important things to keep in mind for our purposes are that users interact with these models via natural language queries, and each time they ask the same question, there could be a variation in the answer.
Optimizing evil twin prompts
Prompt-induced distributions
Given a normal prompt like the one from earlier, “What are some of the risks of AI?”, how can we find a gibberish prompt that elicits the same answers as the normal one? The core idea is that we can take our normal prompt, and feed it into the model hundreds of times to generate a set of answers. Formally, given a prompt $\boldsymbol p \in \mathbb{R}^{k_p \times V}$ consisting of $k_p$ tokens corresponding to the vocabulary $V$, we generate a set of $n$ answers which we refer to as documents, where each document $\boldsymbol d \in \mathbb{R}^{k_d \times V}$ consists of $k_d$ tokens.
Importantly, since we are sampling the documents from the model given the same prompt, we can compute the conditional probability of each document $\boldsymbol d_i, i \in \{1,\ldots,n\}$ given the prompt $\boldsymbol p$. We won’t get into the mathematical formulation of this here, please see the full paper for a much more rigorous setup.
Distance between prompts
Our original goal was to find a gibberish prompt that behaves similarly to a normal user query, so we now frame the problem as the following:
Given two prompts, $\boldsymbol p, \boldsymbol p^* \in \mathbb{R}^{k_p \times V}$, where $\boldsymbol p$ is the user query and $\boldsymbol p^*$ consists of random tokens, we seek to optimize the tokens in $\boldsymbol p^*$ such that when we feed $\boldsymbol p^*$ into the LM, we produce answers that are similar to $\boldsymbol p$.
How do we know if $\boldsymbol p^*$ is similar to $\boldsymbol p$?
For this we draw from principles in information theory, specifically we consider the Kullback-Liebler (KL) Divergence between two distributions. We won’t get into the details of what KL Divergence is or how it works in this post, but intuitively in our case one can think of it as the “distance between two prompts” (i.e., how close in similarity are two prompts based on their typical outputs?). Once again, we don’t reproduce the derivation of the KL Divergence between prompts here, please see our full paper for all the details.
Discrete optimizer
Great! Now we’ve formulated a means of computing a “distance” between two prompts, and obviously minimizing this distance would imply that the two prompts $\boldsymbol p$ and $\boldsymbol p^*$ are functionally similar. How can we actually modify the tokens in $\boldsymbol p^*$ to minimize this distance? Due to the discrete nature of language, we cannot directly solve our problem by typical continuous optimization methods such as gradient descent.
For our answer, we borrow from the adversarial attacks literature. Specifically, we use a discrete optimization algorithm introduced by Zou et al. [1] known as Greedy Coordinate Gradient (GCG). Without going into too much detail, GCG is a variation of a hill-climbing algorithm that replaces a single token at each optimization step with a new token that is more likely to reduce the loss. We run GCG for several hundred iterations, until the KL Divergence between $\boldsymbol p$ and $\boldsymbol p^*$ is near 0.
Finally, we have a new optimized prompt $\boldsymbol p^*$ which is functionally very similar to $\boldsymbol p$, but is totally incomprehensible! For a few examples, please refer to the table at the beginning of this post.
Transferability
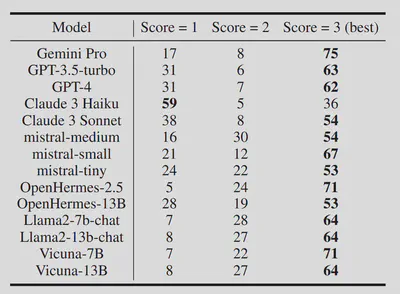
Remarkably, we also find that many of these prompts that we optimize for smaller LMs (such as Llama-2-chat-7b and Vicuna-7b) transfer well to large models! Specifically, we optimize 100 prompts using Vicuna-7b, then feed these into a variety of open source and industrial models, and use GPT-4 as a judge to see if the model outputs from the gibberish prompt seemingly answer the same question as the original prompt. We measure this on a scale of 1-3, and find that the majority of the tested prompts successfully work on models like Claude 3 Sonnet and Gemini Pro.
Get started with our Python package
Our package evil_twins makes it easy for anyone to optimize their own evil twin prompts!
First, install the package via pip:
pip install evil_twins@git+https://github.com/rimon15/evil_twins
Next, let’s import the functionality that we’ll need and load an example supported model.
from evil_twins import load_model_tokenizer, DocDataset, optim_gcg
model_name = "google/gemma-2-2b-it"
model, tokenizer = load_model_tokenizer(model_name, use_flash_attn_2=False)
Now, we can pick our favorite prompt and optimize a twin for it! Note the optim_prompt initialization. In addition to a string starting prompt to optimize, we also support input via a tensor of shape (1, n_toks). For the experiments in our original paper, we used 100 documents with a length of 32 tokens each, but we find that in general, even with 10 tokens, we are able to produce adequate results.
optim_prompt = "x " * 20
dataset = DocDataset(
model=model,
tokenizer=tokenizer,
orig_prompt="What are some of the dangers of AI?",
optim_prompt=optim_prompt,
n_docs=100,
doc_len=10,
gen_batch_size=50,
)
Now we can run the GCG-based optimization and get our results! This will output a log showing the KL, optimized string, and other properties in the specified path. It will also save the best found (via lowest KL) tokenized IDs of shape (1, n_toks).
results, ids = optim_gcg(
model=model,
tokenizer=tokenizer,
dataset=dataset,
n_epochs=500,
kl_every=1,
log_fpath="twin_log.json",
id_save_fpath="twin_ids.pt",
batch_size=4,
top_k=256,
gamma=0.0,
)
Additional resources
Please consider citing our work Prompts have evil twins
References
[1] Andy Zou, Zifan Wang, Nicholas Carlini, Milad Nasr, J. Zico Kolter, Matt Fredrikson. Universal and Transferable Adversarial Attacks on Aligned Language Models